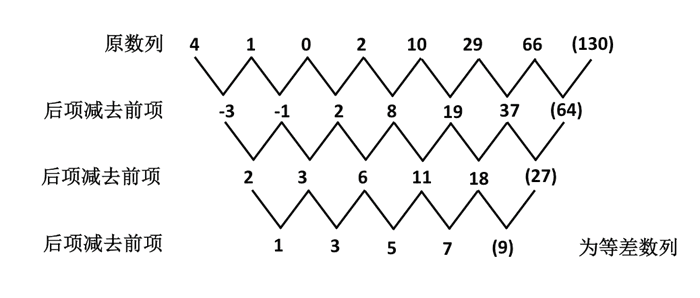
多级数列是数字推理中考查频率最高的题型，每年必考，但难度不高，考查方式相对变化不大，各位需重点掌握。
一、题型特征
没有明显特征的数列
二、解题技巧
1、第一步：优先考虑两两做差或两两做和，不行再考虑除法；如果数字之间成“倍数关系”时，优先做除法。多级数列经过做差、和、积、商之后，得到的一级数列一般都是简单的基础数列。
2、第二步：对一级数列进行观察，如果数列变化无规律（注意一级数列可能是递推数列），可以再进行第一步的操作，得到二级数列。
三、随笔练习
例1：(2019河南司法所) 11、14、23、50、131、()
A.292
B.326
C.356
D.374
解析
数列各项依次增加，无明显特征，所以考虑两两作差，观察结果再求解。
将已知项两两作差，均用后一项数字减前一项数字，可得一级数列：3、9、27、81，此数列是公比为3的等比数列，则其下一项为81×3=243，题干所求项为131+243=374。
选择D选项。
例1：(2017江苏) 4，5，7，16，80，（ ）
A.292
B.326
C.356
D.374
解析
数列各项依次增加，无明显特征，所以考虑两两作差。
后项减前项得到一级数列：1，2，9，64，出现9和64考虑幂次数列，可将新数列转化为10、21、32、43，故一级数列的下一项应为54。
所求项为：80+54，计算尾数为5，只有D项符合 。
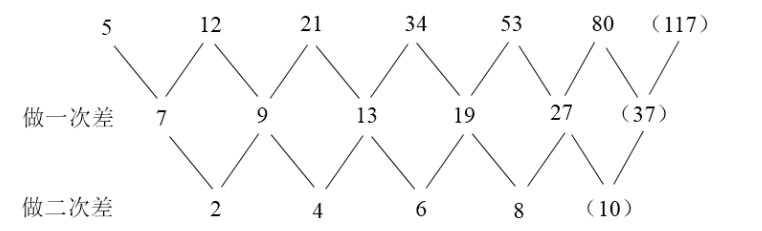
例3：(2009联考) 5，12，21，34，53，80，( )
A.121
B.115
C.119
D.117
解析
- 数列没有明显特征，优先考虑做差，数列没有明显特征，再做差。如图所示：
第二次做差数列是公差为2的等差数列，则二级数列下一项为8+2=10。
一级数列的下一项为27+10=37，所求项为80+37=117。
因此，选择D选项。
例4：(2018广州) 1，2，4，7，12，（ ）
A.18
B.19
C.20
D.21
解析
数列无明显特征且起伏较小，优先考虑作差。
作差后得到新数列为：1、2、3、5、（ ），为递推数列，则新数列下一项为：3+5=8，故所求项为：12+8=20。
注意：作差得到的新数列1、2、3、5、（ ），容易被误判为质数列。但1既不是质数也不是合数，所以新数列不是质数列，不能推断出新数列下一项是7。
故正确答案为C。
例5：(2015联考) 34、41、46、56、64、（ ）、88
A.75
B.77
C.79
D.81
解析
数列起伏较小且无明显特征，考虑作差。
作差后得到新数列7、5、10、8、（ ）、（ ）。
新数列无规律，再次作差后得到新数列为：-2、5、-2、（ ）、（ ）。
考虑为循环数列，因此二次作差后括号中所求数为-2、5、-2、5、-2，则首次作差后得到的一级数列为7、5、10、8、13、11。
原数列括号内=63+13=88-11=77。
故正确答案为B。
例6：(2017广州) 30，16，22，18，19，（ ）
A.16
B.16.5
C.17
D.17.5
解析
数列无明显特征，考虑作差。后项 - 前项，得 -14，6，-1，1，（x）；
再作差，后项 - 前项，得20，-10，5，（y），此数列为公比为 -0.5的等比数列。
因此（y）=5 ×（-0.5）= -2.5，那么（x）= -2.5+1= -1.5，原数列=19-1.5=17.5。
故正确答案为D。
例7：(2014浙江) 1，1，5，7，13，（ ）
A.15
B.17
C.19
D.21
解析
数列起伏不大，考虑作差后并无规律，考虑两两相加。
作和后得到新数列为：2、6、12、20、（x）
数列无明显特征，继续作差后为：4、6、8、（y），为公差为2的等差数列，故下一项为y=8+2=10。
则一级数列括号内应为x=20+10=30。
原数列所求应为30-13=17。
故正确答案为B。
例8：(2018新疆) 3、6、18、72、360、（）
A.2160
B.1800
C.1440
D.432
解析
观察数列，发现两两之间有明显的倍数关系，因此考虑作商。
两两作商，后一项除以前一项得到新数列：2、3、4、5、（），该数列是公差为1的等差数列，故下一项为6，则题干所求项应为6×360=21600。
故正确答案为A。
例9：(2019江苏) 8、2、1、1、2、（）
A.4
B.8
C.10
D.16
解析
观察数列，发现两两之间有明显的倍数关系，例如8与2是4倍关系，2与1是2倍关系，1与1是1倍关系，1与2是12的关系，因此考虑作商。
两两作商，前一项÷后一项得到新数列：4、2、1、 12、()，此数列是公比为12的等比数列，故新数列的下一项为14，则所求项2所求项=14。
所求项=8，故正确答案为B。
例10：(2025浙江) -7，1，11，24，42，67，（ ）
A.103
B.109
C.116
D.122
解析
数列无明显特征，优先考虑多级数列，考虑作差。
后项-前项得到一级数列：8，10，13，18，25，无明显特征。
再次作差，新数列后项-前项得到二级数列：2，3，5，7，是连续质数数列，下一项为11。
则一级数列下一项为25+11=36。
原数列所求项为67+36=103。
故正确答案为A。
例10：(2013浙江) 4，1，0，2，10，29，66，（ ）
A.101
B.116
C.125
D.130
解析
-
- 故正确答案为D。
- 注：此类题型要注意数列项数，项数为8，且无分组规律和交叉规律，则为三级数列，考查较少，难度较大，复习需注意。（若对应7项，则多为二级数列，考查较多）。
